Rugby
An Algorithmic Approach
Rugby is a sport close to my heart. I have always enjoyed watching, playing and discussing this fast-paced game of grit, strategy and strength. I am, however, also an avid fan of computer science, and my upper body strength is not quite what it used to be. I believe that no topic, no matter how interesting, can not be made even more interesting through the use of math, science and algorithms, without any need for upper body strength. Indeed, I will prove that rugby is no exception to this rule.
For the uninitiated, in rugby, there are four types of scores: penalty goal (3 points), drop goal (3 points), try (5 points) and converted try (7 points). It is easy to show that from this, all points totals are possible, except for 1, 2 and 4. In this post, I’ll be answering a bunch of hypothetical questions that can be asked about these scores, and applying algorithms from computer science to do it as efficiently as possible.
To kick off, let’s find out what the minimum number of scoring opportunities a team needs to achieve a specific points total. For example, for a team to reach a score of 8, the minimum number of scoring opportunities they need is two, because they need one try and one penalty or drop goal, and there are no other ways to reach that points total.
We can tackle this problem with a dynamic programming approach. Dynamic programming is a technique by which optimal solutions are first found for smaller sub-problems, and a recurrence relationship then used to calculate the solution for the bigger problems. In this case, we can start by calculating the minimum number of scoring opportunities needed for smaller scores, and use these solutions to build up to bigger scores.
We have already noted that all totals are possible except 1, 2 and 4. We can therefore initialize some data with the minimum number of scoring opportunities needed for certain totals:
- 0 points: 0 opportunities needed
- 1 point: impossible
- 2 points: impossible
- 3 points: 1 scoring opportunity (drop kick or penalty kick)
- 4 points: impossible
- 5 points: 1 scoring opportunity (try)
We can now continue and note that for any total, the minimum number of opportunities must be equal to the minimum for a previous total, plus one extra scoring opportunity needed to reach this new total. For example, to reach 8, the minimum is one extra opportunity (a drop kick, 3 points) plus the minimum for achieving 8-3=5, which happens to be 1. The minimum for 8 is therefore 2. Being the particularly mathematically-inclined rugby enthusiasts that we are, we prefer things in equation form:
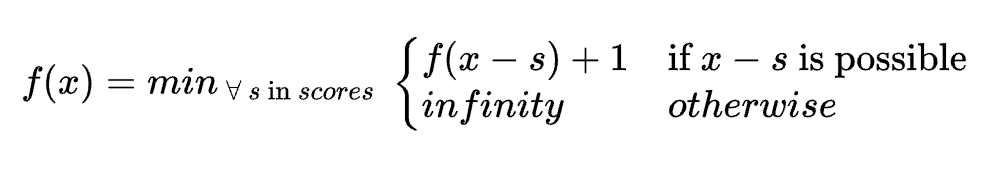
This is where you can see the recurrence relationship clearly; to calculate the solution for a new total points x, for every score s (either 3, 5 or 7), we check the previous minimum totals calculated at x-s and see which one is the minimum needed. If we were to now calculate the minimum for all totals from 1 up to n, we can create a table of minimum scoring opportunities needed in O(n) time and O(n) space. Here is this table up to 20 points:
| Total Points | Minimum Scoring Opportunities |
|---|---|
| 0 | 0 |
| 1 | Impossible |
| 2 | Impossible |
| 3 | 1 |
| 4 | Impossible |
| 5 | 1 |
| 6 | 2 |
| 7 | 1 |
| 8 | 2 |
| 9 | 3 |
| 10 | 2 |
| 11 | 3 |
| 12 | 2 |
| 13 | 3 |
| 14 | 2 |
| 15 | 3 |
| 16 | 4 |
| 17 | 3 |
| 18 | 4 |
| 19 | 3 |
| 20 | 4 |
Putting our algorithm in use, we can see that New Zealand needed a minimum of 21 scoring opportunities in their record-breaking game against Japan in the 1995 World Cup to reach their final points total of 145. This makes it all the more remarkable that they did, indeed, score 21 times, achieving maximum efficiency, something we programmers can surely appreciate (Simon Culhane managed to convert all but one of the 21 tries in that game).
Okay, that was fun! But we’re only warming up. In that silent moment huddling down for a scrum, have you ever wondered, for a given points total, what are all the possible ways was that the game could have played out? I know I have.
Let’s extend our algorithm a bit to answer that question, and find all scoring combinations to achieve any one total score. This is very similar to what we were seeking before, except that now, instead of looking for the minimum number of scoring opportunities, we want to find all the possible combinations of scoring opportunities. For our purposes, it’s okay to assume that a penalty conversion and a drop kick conversion is one and the same, as they amount to the same score of 3.
We can again use a dynamic programming approach, but this time we have to be a little more careful: if we were to simply add the combinations of previous totals to obtain the new total, we might count the same combination twice. For example, for a total of 3 there is only one combination: one penalty (or drop) kick. For a total of 5, there is also only combination: one try. Following our earlier algorithm, for a total of 8, then, we could look at the score 8-5=3, and find one combination. Next we look at 8-3=5, finding one combination again. We then look at 8-7=1, which has no combinations. So the total combinations is two. Right? Wrong! In using this dynamic programming shortcut, we accidentally counted the same combination twice: 3+5, and 5+3, which we consider to be the same thing. A total of 8 points can have only one combination, a try and a penalty kick. Therefore, we need to keep track of the combinations we found before, and ensure that any new combination we add is unique. Luckily this isn’t so bad, and in running our algorithm we can optimize memory by only keeping track of the combinations we found at 4 positions: i, the current total, i-3, i-5 and i-7. From these combinations we can build all possible unique combinations for i. You can see an implementation of this in Go by reading the source code for this post.
With the results calculated, let’s see the table of combinations for all the scores up to 20!
| Score | Kicks | Tries | Tries + Conversions |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 5 | 0 | 1 | 0 |
| 6 | 2 | 0 | 0 |
| 7 | 0 | 0 | 1 |
| 8 | 1 | 1 | 0 |
| 9 | 3 | 0 | 0 |
| 10 | 1 | 0 | 1 |
| 0 | 2 | 0 | |
| 11 | 2 | 1 | 0 |
| 12 | 4 | 0 | 0 |
| 0 | 1 | 1 | |
| 13 | 2 | 0 | 1 |
| 1 | 2 | 0 | |
| 14 | 3 | 1 | 0 |
| 0 | 0 | 2 | |
| 15 | 5 | 0 | 0 |
| 1 | 1 | 1 | |
| 0 | 3 | 0 | |
| 16 | 3 | 0 | 1 |
| 2 | 2 | 0 | |
| 17 | 4 | 1 | 0 |
| 1 | 0 | 2 | |
| 0 | 2 | 1 | |
| 18 | 6 | 0 | 0 |
| 2 | 1 | 1 | |
| 1 | 3 | 0 | |
| 19 | 4 | 0 | 1 |
| 3 | 2 | 0 | |
| 0 | 1 | 2 | |
| 20 | 5 | 1 | 0 |
| 2 | 0 | 2 | |
| 1 | 2 | 1 | |
| 0 | 4 | 0 |
From this table we can see that for a points total of 20, four different combinations are possible: 5 kicks and 1 try, 2 kicks and 2 converted tries, 1 kick, 2 tries and 1 converted try, or 4 tries. If we let the program run up to 145, the same highest score in a test match by New Zealand we saw earlier, we see that there were 119 different ways that the match could have played out so that New Zealand still ended on 145.
And we haven’t even talked about permutations! How many ways could that famous game have played out to reach the same 145 points total? In other words, in how many ways can we order each of the combinations to get the same result? If we have a game with 8 points total, a try and a penalty kick, that game could have played out in two ways: either first the try and then the penalty kick, or first the penalty kick, then the try. We can easily adapt our solution from the previous question to answer this for any total, but the numbers will grow very big very fast. I’ll leave this as an “exercise for the reader” ;)
What have we learnt?
Algorithms make everything more interesting.
To score a total of 145, you need to score at least 21 times.
The 1995 New Zealand World Cup Team were both formidable and efficient, and would make good computer scientists.
Dynamic programming is a useful technique in your programming toolkit.
You can find the full source code for this post here.